C++ LCA (最小共通祖先)

#include <cassert>
#include <cmath>
#include <iostream>
#include <vector>

using namespace std;

const int M = 100001;
vector<vector<int>> graph(M);

struct LCA {
  int root;
  const int n;
  const int log2_n;
  vector<vector<int>> parent;
  vector<int> depth;

  // n : 頂点数
  LCA(const vector<vector<int>>& graph, int root, int n)
    : root(root), n(n), log2_n(log2(n)+1), parent(log2_n, vector<int>(n)), depth(n) {
      dfs(graph, root, root, 1);
      for (int k = 0; k+1 < log2_n; ++k) {
        parent.push_back(vector<int>(n, root)); // 要素数n, 値rootで初期化
        for (int v = n-1; v >= 0; --v) {
          int par = parent[k][v];
          parent[k+1][v] = parent[k][par];
        }
      }
    }
  
  /** 
   * par : 親のid
   * d : 木の深さ (1から始める)
   */ 
  void dfs(const vector<vector<int>>& graph, int from, int par, int d) {
    parent[0][from] = par;
    depth[from] = d;
    for (int to: graph[from]) {
      if (depth[to] > 0) continue;
      dfs(graph, to, from, d+1);
    }
  }


  int get(int v1, int v2) {
    // 深さが同じになるまで片方を登らせる
    if (depth[v1] < depth[v2]) swap(v1, v2);
    for (int k = 0; k < log2_n; ++k) {
      if ((depth[v1]-depth[v2]) >> k & 1) {
        v1 = parent[k][v1];
      }
    }
    if (v1 == v2) return v1;

    // 親が同じになる直前まで登らせる
    for (int k = log2_n-1; k >= 0; --k) {
      int p_v1 = parent[k][v1];
      int p_v2 = parent[k][v2];
      if (p_v1 == p_v2) continue;
      v1 = p_v1;
      v2 = p_v2;
    }
    assert(parent[0][v1] == parent[0][v2]);
    return parent[0][v1];
  }
};

int main() {
  /*
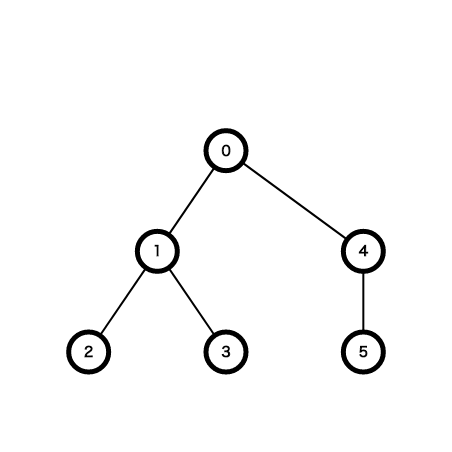
   *     0
   *   1   4
   *  2 3  5
   */
  int n = 6;
  graph[0].push_back(1);
  graph[1].push_back(2);
  graph[1].push_back(3);
  graph[0].push_back(4);
  graph[4].push_back(5);

  int root = 0;
  LCA lca = LCA(graph, root, n);
  cerr << "lca of (2, 0) is " << lca.get(2, 0) << endl;
  cerr << "lca of (2, 3) is " << lca.get(2, 3) << endl;
  cerr << "lca of (2, 4) is " << lca.get(2, 4) << endl;
  cerr << "lca of (4, 5) is " << lca.get(4, 5) << endl;
}

% g++ -std=gnu++1y -O2 lca.cpp -o lca
% ./lca
lca of (2, 0) is 0
lca of (2, 3) is 1
lca of (2, 4) is 0
lca of (4, 5) is 4