C++ トポロジカルソート

#include <cassert>
#include <iostream>
#include <stack>
#include <vector>

using namespace std;

// FIXME: graphをグローバル変数にしているのどうにかしたい
vector<int> graph[200010];

bool topologicalSort(int V, int E, vector<int> &order) {
  assert(order.size() == 0);
  // トポロジカルソートした結果をorderに格納して返す. 返り値はDAGならtrue
  vector<int> indegree(V); // 200000とかだと遅い？ 厳しそうならグローバル変数にする
  // 入次数の初期化. ほんとは読み込み時にやったほうが効率が良いけど許容する
  for (int v = 0; v < V; ++v) {
    for (int nv : graph[v]) ++indegree[nv];
  }

  stack<int> st;
  for (int v = 0; v < V; ++v) {
    // 入次数0の点をstackにいれる
    if (indegree[v] == 0) st.push(v);
  }

  while (st.size() > 0) { 
    int v = st.top(); st.pop();
    order.push_back(v);
    for (int nv : graph[v]) {
      --indegree[nv];
      if (indegree[nv] == 0) st.push(nv);
    }
  }

  return order.size() == V;
}

// vector
template<typename T> ostream& operator<<(ostream& s, const vector<T>& v) {
  int len = v.size();
  for (int i = 0; i < len; ++i) {
    s << v[i]; if (i < len - 1) s << " ";
  }
  return s;
}

int main() {
  int V, E;
  cin >> V >> E;
  for (int i = 0; i < E; ++i) {
    int a, b;
    // 0-indexとする
    cin >> a >> b;
    // 点a -> 点bの辺をはる
    graph[a].push_back(b);
  }
  vector<int> order;
  bool is_dag = topologicalSort(V, E, order);

  cout << "This graph is ";
  if (is_dag) { cout << "DAG" << endl; }
  else { cout << "not DAG" << endl; }
  cout << order << endl;
}

% g++ -std=gnu++1y -O2 topological-sort.cpp -o run
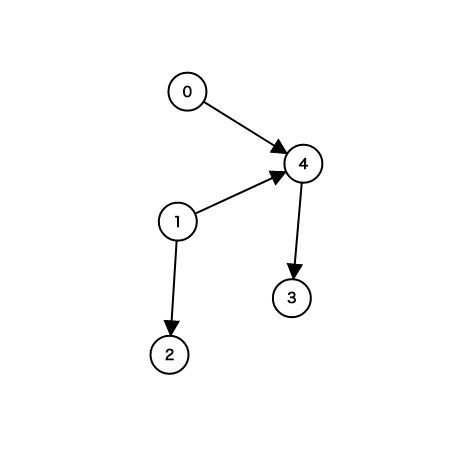
% cat 1.in
5 4
0 4
1 4
1 2
4 3
% ./run < 1.in
This graph is DAG
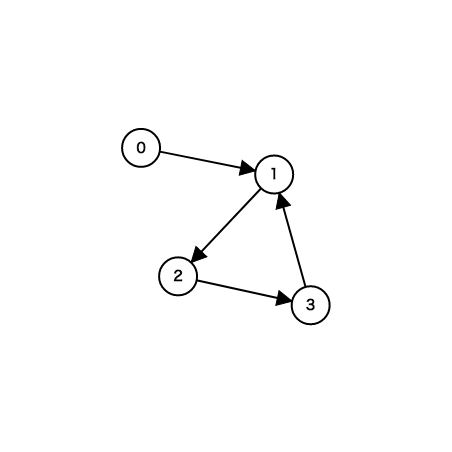
1 2 0 4 3

% cat 2.in
4 4
0 1
1 2
2 3
3 1
% ./run < 2.in
This graph is not DAG
0